6th Grade Math
Study Guides/Tutorials:
One-Step Equations with Rational Coefficients Study Guide(2).pdf
GCF:
GCF with Prime factorization.gif
Adjacent, Supplementary, Complementary, and Vertical Angles Study Guide_000080.pdf
Order of Operations with Exponents_0001.pdf
Simple Interest Study Guide_000058.pdf
Addition and Subtraction of Integer Rules.jpg
Find the GCF
GCF stands for Greatest Common Factor. Factors are numbers multiplied together. Sometimes, it’s necessary to know the GCF of 2 or more numbers. Why? I’m glad you asked. Basically, the GCF helps to efficiently and quickly reduce fractions. One way to determine the GCF is simply by prime factorization.
Example: 12 & 36 Find their GCF's
Step 1: Find the Prime factors for
12: 2 x 2 x 3
36: 2 x 2 x 3 x 3
Step 2: Multiply each factor that has a match
GCF = 2 x 2 x 3 = 12
Example: Find the GCF for 48 and 72
Step 1: Find the prime factors for
48: 2 x 2 x 2 x 2 x 3
72: 2 x 2 x 2 x 3 x 3
Step 2: Multiply each factor that has a match
GCF = 2 x 2 x 2 x 3 = 24
Example: Find the GCF for 56, 70, and 98
Step 1: Find the prime factors for
56: 2 x 2 x 2 x 7
70: 2 x 5 x 7
98: 2 x 7 x 7
Step 2: Multiply each factor that has a match in all 3 numbers
GCF = 2 x 7 = 14
Customary Measures:
Customary Units of Measurement Chart_000062.pdf
Customary Units of Measure Comparisons_000063.pdf
Variable Expressions Study Guide _000079.pdf
Variables and Equations_000087.pdf
Two-Step Equations Study Guide_000089.pdf
Scientific Notation Study Guide_0001.pdf
How to Solve One-Step Equation.pdf
How to solve multi-step equations:
-
Solve –5x – 7 = 108
In this equation, the variable (on the left-hand side) is multiplied by a minus five, and then a seven is subtracted from it. In hopes (as always!) of avoiding fractions, I'll add seven to either side of the equation first. Only then will I divide through by the minus five. My work looks like this:
-5x - 7 = 108
+7 +7
-------------
-5x = 115
--- ---
-5 -5
x = -23
I've shown my work neatly. Now I'll clearly rewrite my solution at the end of my work:
x = –23
-
Solve 3x – 9 = 33
The variable (on the left-hand side of the equation) is multiplied by a three, and then a nine is subtracted from it. I'll take care of the nine first, and then the three:
3x - 9 = 33
+9 +9
-----------
3x = 42
-- --
3 3
x = 14
In this case, again, my solution has no fractions:
x = 14
-
Solve 5x + 7x = 72
In this equation, I have two terms on the left-hand side that contain variables. So my first step is to combine these "like terms" on the left. Then I can solve:
5x + 7x = 12x
So now my equation is:
12x = 72
Even though it might initially have looked more complicated, this is actually a one-step equation. I'll solve by dividing through by twelve:
12x = 72
--- --
12 12
x = 6
My answer is:
x = 6
-
Solve 4x – 6 = 6x
In this equation, I've got terms with variables on either side of the equation. To solve, I need to get those variable terms all on one side of the equation.
There is no rule saying which of the two terms I should move, the 4x or the 6x. However, I've learned from experience that, to avoid negative coefficients on my variables, I should move the x term with the smaller coefficient. That means, in this case, that I'll subtract the 4x from the left-hand side over to the right-hand side:
4x - 6 = 6x
-4x -4x
-------------
-6 = 2x
And now I have a one-step equation, which I'll solve by dividing through by two:
-6 = 2x
-- --
2 2
-3 = x
My solution is:
x = –3
How to solve inequalities:
Sometimes we need to solve Inequalities like these:
|
Symbol
|
Words
|
Example
|
|---|---|---|
| > |
greater than
|
x + 3 > 2
|
| < |
less than
|
7x < 28
|
| ≥ |
greater than or equal to
|
5 ≥ x - 1
|
| ≤ |
less than or equal to
|
2y + 1 ≤ 7
|
NOTE:
- When solving inequalities by addition and subtraction you clear out to isolate the variable just as you did in the prior equality lessons.
- The inequalities are solved the same way. Only difference is when you multiple or divide by a negative number that’s next to the variable then you have to flip the inequality. Meaning if you’re coefficient is negative your greater than becomes less then or you’re less then becomes greater than.
- Read the attached Study Guide on Properties of Inequalites:
Properties of Inequality Study Guide.pdf
Solving:
Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:
| Something like: | x < 5 | |
| or: | y ≥ 11 |
We call that "solved".
Example: x + 2 > 12
Subtract 2 from both sides:
x + 2 − 2 > 12 − 2
Simplify:
x > 10
Solved!
How to Solve
Solving inequalities is very like solving equations ... we do most of the same things ...
... but we must also pay attention to the direction of the inequality.
Direction: Which way the arrow "points"
Some things can change the direction!
< becomes >
> becomes <
≤ becomes ≥
≥ becomes ≤
Safe Things To Do
These things do not affect the direction of the inequality:
- Add (or subtract) a number from both sides
- Multiply (or divide) both sides by a positive number
- Simplify a side
Example: 3x < 7+3
We can simplify 7+3 without affecting the inequality:
3x < 10
But these things do change the direction of the inequality ("<" becomes ">" for example):
- Multiply (or divide) both sides by a negative number
- Swapping left and right hand sides
Example: 2y+7 < 12
When we swap the left and right hand sides, we must also change the direction of the inequality:
12 > 2y+7
Here are the details:
Adding or Subtracting a Value
We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra), like this:
Solve: x + 3 < 7
If we subtract 3 from both sides, we get:
x + 3 - 3 < 7 - 3
x < 4
And that is our solution: x < 4
In other words, x can be any value less than 4.
What did we do?
|
We went from this:
To this: |
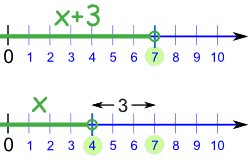 |
x+3 < 7
x < 4 |
||
And that works well for adding and subtracting, because if we add (or subtract) the same amount from both sides, it does not affect the inequality
Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.
What If I Solve It, But "x" Is On The Right?
No matter, just swap sides, but reverse the sign so it still "points at" the correct value!
Example: 12 < x + 5
If we subtract 5 from both sides, we get:
12 - 5 < x + 5 - 5
7 < x
That is a solution!
But it is normal to put "x" on the left hand side ...
... so let us flip sides (and the inequality sign!):
x > 7
Do you see how the inequality sign still "points at" the smaller value (7) ?
And that is our solution: x > 7
Note: "x" can be on the right, but people usually like to see it on the left hand side.
Multiplying or Dividing by a Value
Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying).
But we need to be a bit more careful (as you will see).
Positive Values
Everything is fine if we want to multiply or divide by a positive number:
Solve: 3y < 15
If we divide both sides by 3 we get:
3y/3 < 15/3
y < 5
And that is our solution: y < 5
Negative Values
| When we multiply or divide by a negative number we must reverse the inequality. |
Why?
Well, just look at the number line!
For example, from 3 to 7 is an increase,
but from -3 to -7 is a decrease.
 |
|
| -7 < -3 | 7 > 3 |
See how the inequality sign reverses (from < to >) ?
Let us try an example:
Solve: -2y < -8
Let us divide both sides by -2 ... and reverse the inequality!
-2y < -8
-2y/-2 > -8/-2
y > 4
And that is the correct solution: y > 4
(Note that I reversed the inequality on the same line I divided by the negative number.)
So, just remember:
